1.5. Chủ đề 5: Hình học phẳng-Tỉ số lượng giác của góc nhọn. Một số hệ thức về cạnh và góc trong tam giác vuông.
1.5. Chủ đề 5: Hình học phẳng
TT - 1 - Tỉ số lượng giác của góc nhọn. Một số hệ thức về cạnh và góc trong tam giác vuông.
TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN
1. Tỉ số lượng giác của góc nhọn
Cho góc nhọn \(0^\circ < \alpha < 90^\circ\). Xét ABC vuông tại A có \(\widehat {ABC} = \alpha \)
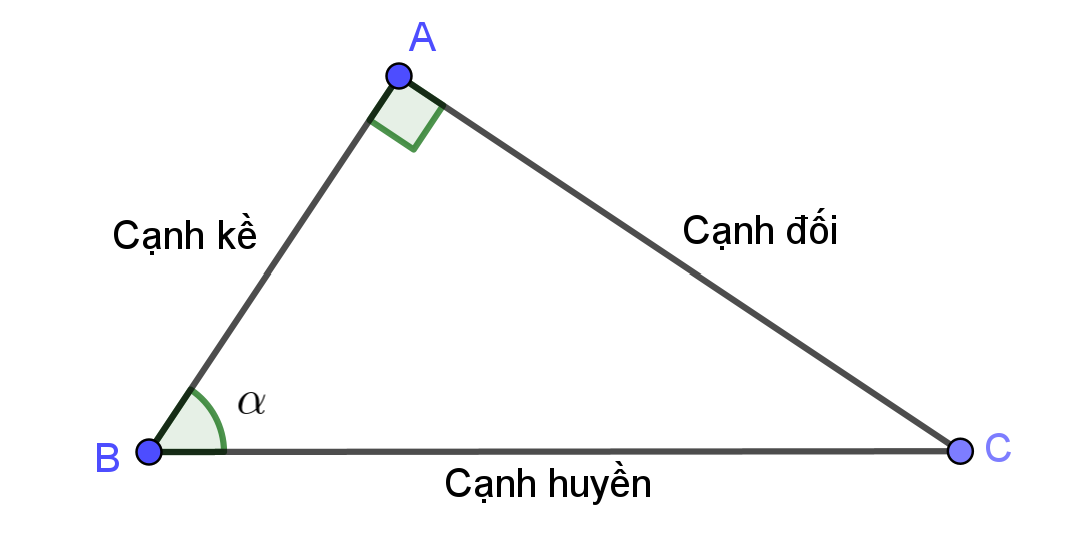
Các tỉ số lượng giác của góc nhọn \(\alpha\):
Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc \(\alpha\), kí hiệu \(\sin\alpha\)
\(\sin\alpha = \dfrac{AC}{BC}\)
Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin của góc \(\alpha\), kí hiệu \(\cos\alpha\)
\(\cos\alpha = \dfrac{AB}{BC}\)
Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc \(\alpha\), kí hiệu \(\tan\alpha\)
\(\tan\alpha = \dfrac{AC}{AB}\)
Tỉ số giữa cạnh kề và cạnh đối được gọi là côtang của góc \(\alpha\), kí hiệu \(\cot\alpha\)
\(\cot\alpha = \dfrac{AB}{AC}\)
Chú ý: Với góc nhọn \(\alpha\), ta có:
\(0 < \sin\alpha < 1; 0 < \cos\alpha < 1\)
\(\cot\alpha = \dfrac{1}{\tan\alpha}\)
2. Tỉ số lượng giác của hai góc phụ nhau
Hai góc phụ nhau là hai góc nhọn có tổng bằng \(90^\circ\).
Định lí: Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
Nhận xét: Với \(0^\circ < \alpha < 90^\circ\), ta có:
\(\sin(90^\circ - \alpha) = \cos\alpha\)
\(\cos(90^\circ - \alpha) = \sin\alpha\)
\(\tan(90^\circ - \alpha) = \cot\alpha\)
\(\cot(90^\circ - \alpha) = \tan\alpha\)
Bảng tỉ số lượng giác của một số góc đặc biệt:
| \(\alpha \) | \(30^\circ\) | \(45^\circ\) | \(60^\circ\) |
|---|---|---|---|
| \(\sin\alpha\) | \(\dfrac{1}{2}\) | \(\dfrac{\sqrt{2}}{2}\) | \(\dfrac{\sqrt{3}}{2}\) |
| \(\cos\alpha\) | \(\dfrac{\sqrt{3}}{2}\) | \(\dfrac{\sqrt{2}}{2}\) | \(\dfrac{1}{2}\) |
| \(\tan\alpha\) | \(\dfrac{1}{\sqrt{3}}\) | \(1\) | \(\sqrt{3}\) |
| \(\cot\alpha\) | \(\sqrt{3}\) | \(1\) | \(\dfrac{1}{\sqrt{3}}\) |
DẠNG 1. TÍNH TỈ SỐ LƯỢNG GIÁC
Với góc nhọn \(\alpha\), ta có:
\(0 < \sin\alpha < 1; 0 < \cos\alpha < 1\)
\(\cot\alpha = \dfrac{1}{\tan\alpha}\)
\(\tan\alpha = \dfrac{\sin\alpha}{\cos\alpha}\)
\(\cot\alpha = \dfrac{\cos\alpha}{\sin\alpha}\)
\(\sin^2\alpha + \cos^2\alpha = 1\)
\(\tan\alpha \cdot \cot\alpha = 1\)
\(1 + \tan^2\alpha = \dfrac{1}{\cos^2\alpha}\)
\(1 + \cot^2\alpha = \dfrac{1}{\sin^2\alpha}\)
Bài 1. Tìm các tỉ số lượng giác còn lại của góc α, biết:
a) \(\sin\alpha = \dfrac{3}{5}\)
b) \(\cos\alpha = \dfrac{12}{13}\)
c) \(\tan\alpha = \dfrac{4}{3}\)
Bài 2. Tìm góc nhọn α, biết:
a) \(\sin\alpha = \cos\alpha\)
b) \(\tan\alpha = \cot\alpha\)
Bài 3. Tính giá trị của các biểu thức sau
a) \(A = 4 \cdot \sin^2 45^\circ + 2\cos^2 60^\circ + 3\cot^3 45^\circ\)
b) \(B = \tan 45^\circ \cdot \cos 30^\circ \cdot \cot 30^\circ\)
c) \(C = \cos^2 15^\circ + \cos^2 25^\circ + ... + \cos^2 75^\circ\)
d) \(D = \sin^2 10^\circ + \sin^2 20^\circ + ... + \sin^2 80^\circ\)
BÀI TẬP RÈN LUYỆN
Bài 4. Tính giá trị của các biểu thức sau
a) \(A = \dfrac{{\sin {{30}^o} + 2\cos {{45}^o} - 3{{\tan }^{2026}}{{45}^o}}}{{\cos {{60}^o}}}\)
b) \(B = \dfrac{\sin 30^\circ \cdot \cos 60^\circ \cdot \cot 60^\circ}{\tan 45^\circ}\)
Bài 5. Cho \(\alpha\) là góc nhọn, biết \(\sin\alpha = \dfrac{3}{5}\). Tính \(\cos\alpha\); \(\tan\alpha\); \(\cot\alpha\)
Bài 6.
a) Tính giá trị biểu thức \(A = \cos^2 20^\circ + \cos^2 40^\circ + \cos^2 50^\circ + \cos^2 70^\circ\).
b) Rút gọn biểu thức \(B = \sin 35^\circ + \sin 67^\circ + \cos 23^\circ + \cos 55^\circ\).
Bài 7. Sắp xếp các tỉ số lượng giác sau theo thứ tự tăng dần.
a) \(\sin 70^\circ\), \(\cos 30^\circ\), \(\cos 40^\circ\), \(\sin 51^\circ\)
b) \(\sin 20^\circ\), \(\cos 31^\circ\), \(\cos 47^\circ\), \(\sin 14^\circ\).
c) \(\tan 30^\circ\), \(\cot 34^\circ\), \(\cot 46^\circ\), \(\tan 81^\circ\)
d) \(\cot 25^\circ\), \(\tan 65^\circ\), \(\cot 35^\circ\), \(\tan 75^\circ\).
Bài 8. Cho \(\tan\alpha = 2\). Tính \(A = \dfrac{\sin\alpha + \cos\alpha}{\sin\alpha - \cos\alpha}\)
Bài 9. Biết \(\tan\alpha = 2\). Tính giá trị của biểu thức: \(A = \sin^2\alpha + 2\sin\alpha \cdot \cos\alpha + 3\cos^2\alpha\).
Bài 10. Cho \(\alpha\) là góc nhọn, tính giá trị của biểu thức \(E = \sin^6\alpha + 3\sin^2\alpha \cdot \cos^2\alpha + \cos^6\alpha\)
DẠNG 2. TÍNH TỈ SỐ LƯỢNG GIÁC TRONG TAM GIÁC VUÔNG
Bài 1. Cho tam giác ABC vuông tại C có \(BC = 1,2cm\); \(AC = 0,9cm\). Tính các tỉ số lượng giác của góc \(B\), từ đó suy ra tỉ số lượng giác của góc \(A\).
Bài 2. Cho tam giác ABC có \(AB = a\sqrt{5}\), \(BC = a\sqrt{3}\), \(AC = a\sqrt{2}\)
a) Chứng minh tam giác ABC vuông
b) Tính các tỉ số lượng giác của góc \(B\), từ đó suy ra các tỉ số lượng giác của góc \(A\)
BÀI TẬP RÈN LUYỆN
Bài 3. Cho tam giác ABC vuông tại A có \(AB = 1,6cm\); \(AC = 1,2cm\). Tính các tỉ số lượng giác của góc \(B\), từ đó suy ra tỉ số lượng giác của góc \(C\).
Bài 4. Cho tam giác ABC vuông tại A có \(AB = 60mm\); \(AC = 8cm\). Tính các tỉ số lượng giác của góc \(B\). Từ đó suy ra tỉ số lượng giác của góc \(C\).
Bài 5. Cho tam giác ABC vuông tại A. Hãy tính các tỉ số lượng giác của góc C biết rằng \(\cos B = 0,6\)
Bài 6. Cho tam giác ABC vuông tại A, đường cao AH. Tính \(\sin B\), \(\sin C\)
a) \(AB = 13cm\), \(BH = 5cm\)
b) \(BH = 3cm\), \(CH = 4cm\)
DẠNG 3. BÀI TOÁN THỰC TẾ
Bài 1. Một cây cau có chiều cao 6m. Để hái một buồng cau xuống, phải đặt thang tre sao cho đầu thang tre đạt độ cao đó, khi đó góc của thang tre với mặt đất là bao nhiêu, biết chiếc thang dài 8m (làm tròn đến phút).
Bài 2. Một cột đèn điện AB cao 6m có bóng in trên mặt đất là AC dài 3,5m. Hãy tính \(\angle BCA\) (làm tròn đến phút) mà tia nắng mặt trời tạo với mặt đất.
Bài 3. Tia nắng chiếu qua nóc của tòa nhà hợp với mặt đất một góc \(\alpha\). Cho biết tòa nhà cao 21m và bóng của nó trên mặt đất dài 15m. Tính góc \(\alpha\) (làm tròn đến phút).
Bài 4. Một cái thang dài 6m được đặt dựa vào một bức tường sao cho chân thang cách tường 3m. Tính góc \(\alpha\) tạo bởi thang với bức tường.
Bài 5. Một máy bay đang bay ở độ cao 12 km. Khi bay hạ cánh xuống mặt đất, đường đi của máy bay tạo một góc nghiêng so với mặt đất. Nếu cách sân bay 320 km máy bay bắt đầu hạ cánh thì góc nghiêng là bao nhiêu (làm tròn đến phút)?
DẠNG 4. CHỨNG MINH ĐẲNG THỨC
Bài 1. Cho tam giác ABC vuông tại A \((AB \perp AC)\), \(C = \alpha = 45°\), đường trung tuyến AM, đường cao AH, \(MA = MB = MC = a\). Chứng minh rằng:
a) \(\sin 2\alpha = 2\sin \alpha \cdot \cos \alpha\)
b) \(1 - \cos 2\alpha = 2\cos^2 \alpha\)
c) \(1 - \cos 2\alpha = 2\sin^2 \alpha\)
Bài 2. Cho tam giác nhọn ABC hai đường cao AD và BE cắt nhau tại H. Biết \(\dfrac{HD}{HA} = \dfrac{1}{2}\). Chứng minh rằng \(\tan B \cdot \cot C = 3\).
Bài 3. Cho tam giác ABC có \(BC = a\), \(AC = b\), \(AB = c\). Chứng minh rằng: \(\sin \dfrac{A}{2} = \dfrac{a}{b + c}\).
Bài 4. Cho tam giác ABC có ba góc nhọn, \(BC = a\), \(AC = b\), \(AB = c\). Chứng minh rằng:
\(\dfrac{a}{\sin A} = \dfrac{b}{\sin B} = \dfrac{c}{\sin C}\).
Bài 5. Cho ABC vuông tại A, Chứng minh rằng: \(\dfrac{AC}{AB} = \dfrac{\sin B}{\sin C}\).
