Bài tập tự luận xét tính đơn điệu của hàm số

Ví dụ 1.1. Xét tính đơn điệu của hàm số \(y = 4x^3 + 3x^2 - 36x + 6\).

Ví dụ 1.2. Xét tính đơn điệu của hàm số \(f(x) = \dfrac{x-1}{x+1}\).

Ví dụ 1.3. Xét tính đơn điệu của hàm số \(y = \sqrt{-x^2 + 4}\).

Ví dụ 1.4. Xét tính đơn điệu của hàm số \(y = \log_3(x^2 - 2x)\).

Ví dụ 2.1. Cho hàm số \(y = f(x)\) xác định trên \(\mathbb{R}\) và có bảng biến thiên như sau:

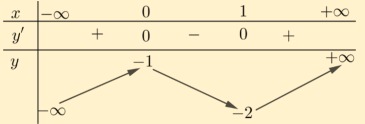
Xét tính đơn điệu của hàm số \(y = f(x)\).

Ví dụ 2.2. Cho hàm số \(y = f(x)\) liên tục trên đoạn \([-3;3]\) và có đồ thị như hình bên. 

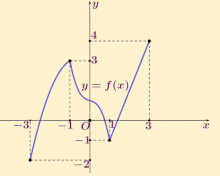
Xét tính đơn điệu của hàm số \(y = f(x)\).

Ví dụ 3.1. Tìm cực trị của hàm số \(y = 2x^3 - 3x^2 + 1\).

Ví dụ 3.2. Tìm cực trị của hàm số \(y = -x^3 + 2x^2 - 2x - 1\).

Ví dụ 3.3. Tìm cực trị của hàm số \(y = \dfrac{x + 2}{3x - 1}\).

Ví dụ 3.4. Tìm cực trị của hàm số \(y = \dfrac{x^2 - 4x + 4}{1 - x}\).

Ví dụ 3.5. Tìm cực trị của hàm số \(f(x) = 2^{x^2 - 5x}\).

Ví dụ 4.1. Cho hàm số \(y = f(x)\) có đạo hàm trên \(\mathbb{R}\) và đồ thị hàm số \(y = f'(x)\) như hình bên. 

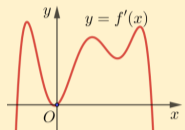
Đồ thị hàm số \(y = f(x)\) bao nhiêu có điểm cực tiểu và điểm cực đại?

Ví dụ 4.2. Cho hàm số \(y = f(x)\) có bảng biến thiên như sau:

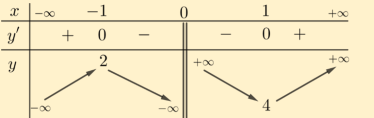
Hàm số \(y = f(x)\) bao nhiêu có điểm cực tiểu và điểm cực đại?

Ví dụ 4.3. Cho hàm số \(y = f(x) = ax^3 + bx^2 + cx + d\) có bảng biến thiên như sau:

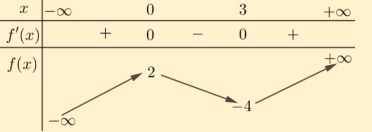
Dựa vào bảng biến thiên, hãy thiết lập công thức hàm số \(y = f(x)\) đã cho?

Ví dụ 5.1. Trong 8 phút đầu kể từ khi xuất phát, độ cao \(h\) (tính bằng mét) của khinh khí cầu vào thời điểm \(t\) phút được cho bởi \(h(t) = 6t^3 - 81t^2 + 324t\). Đồ thị của hàm số \(h(t)\) được biểu diễn như hình bên. 

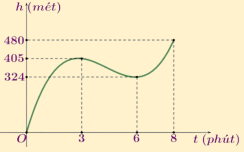
Trong các khoảng thời gian nào khinh khí cầu tăng dần độ cao, giảm dần độ cao?