BÀI 2: VẬN TỐC, GIA TỐC TRONG DAO ĐỘNG ĐIỀU HÒA
BÀI 2: VẬN TỐC, GIA TỐC TRONG DAO ĐỘNG ĐIỀU HÒA
II. VẬN TỐC CỦA VẬT DAO ĐỘNG ĐIỀU HÒA
1. Phương trình của vận tốc
\(v = x' = -ωA sin(ωt + φ)\) hoặc
\(v = ωA cos(ωt + φ + π/2)\)
(Độ lớn vận tốc cực đại: \(v_{max} = ωA\))
2. Đặc điểm của vận tốc
Vận tốc của vật dao động cùng tần số góc, sớm pha \(\dfrac{\pi}{2}\) so với li độ (v và x vuông pha)
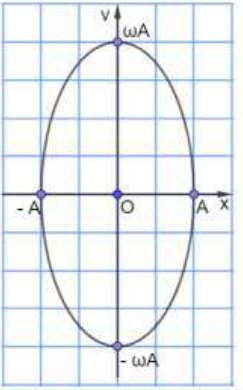
Hệ thức quan hệ giữa vận tốc và li độ (Hệ thức vuông pha)
\(\dfrac{x^2}{A^2} + \dfrac{v^2}{v_{max}^2} = 1 \Rightarrow A^2 = x^2 + \dfrac{v^2}{\omega^2} \Rightarrow v = \pm\omega\sqrt{A^2 - x^2}\)
[Đồ thị quan hệ giữa vận tốc v theo li độ x là 1 đường Elip]
Các trường hợp đặc biệt
\(|x| = \dfrac{A}{2} \Leftrightarrow |v| = \dfrac{v_{max}\sqrt{3}}{2}\)
\(|x| = \dfrac{A\sqrt{3}}{2} \Leftrightarrow |v| = \dfrac{v_{max}}{2}\)
\(|x| = \dfrac{A\sqrt{2}}{2} \Leftrightarrow |v| = \dfrac{v_{max}\sqrt{2}}{2}\)
Khi vật qua VTCB theo chiều dương thì vận tốc cực đại (tốc độ cực đại).
Khi vật qua VTCB theo chiều âm thì vận tốc cực tiểu (nhưng tốc độ cực đại).
Khi vật qua vị trí biên (biên âm hoặc biên dương) thì vận tốc bằng 0 (tốc độ cực tiểu).
Khi vật đi từ VTCB ra biên (âm hoặc dương) thì tốc độ giảm → chuyển động chậm dần
Khi vật đi từ biên (âm hoặc dương) về VTCB thì tốc độ tăng dần → chuyển động nhanh dần.
Lưu ý: Trong dao động điều hòa, không có chuyển động nhanh dần đều hay chậm dần đều. Chỉ có chuyển động nhanh dần và chậm dần.
3. Đồ thị vận tốc theo thời gian
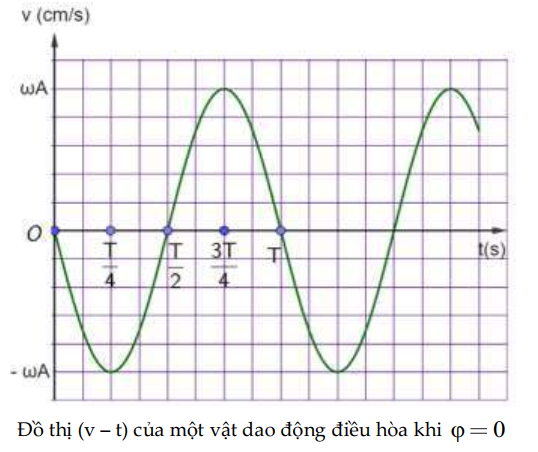
① Từ 0 → \(\dfrac{T}{4}\):
• Vận tốc tăng dần từ 0 đến cực đại dương.
• Nghĩa là vật đang đi ngược chiều dương, vì vận tốc âm.
• Nhưng vì độ lớn vận tốc tăng lên, nên gọi là nhanh dần.
• Vị trí vật lúc này: Từ biên dương về vị trí cân bằng.
② Từ \(\dfrac{T}{4}\) → \(\dfrac{T}{2}\):
• Vận tốc giảm dần từ cực đại dương về 0.
• Vật tiếp tục chuyển động ngược chiều dương, nhưng chậm dần.
• Vị trí vật: Từ vị trí cân bằng đi về biên âm.
③ Từ \(\dfrac{T}{2}\) → \(\dfrac{3T}{4}\):
• Vận tốc tăng dần từ 0 đến cực đại âm.
• Dấu âm cho thấy vật đang chuyển động theo chiều dương.
• Nhưng vì độ lớn vận tốc tăng, nên là nhanh dần.
• Vị trí vật: Từ biên âm về vị trí cân bằng.
④ Từ \(\dfrac{3T}{4}\) → T:
• Vận tốc giảm từ cực đại âm về 0.
• Nghĩa là vật vẫn theo chiều dương, nhưng đang chậm lại.
• Vị trí vật: Từ vị trí cân bằng về biên dương.
Bài Tập Ví Dụ:
Ví dụ 1: Hình bên là đồ thị li độ - thời gian của một vật dao động điều hòa. Dựa vào đồ thị để tính các đại lượng sau:
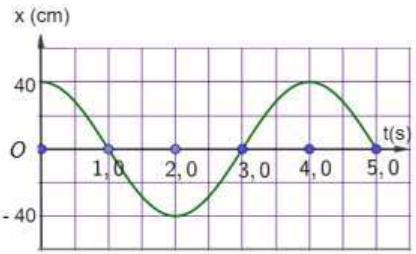
a) Tốc độ của vật ở thời điểm t = 0s.
b) Tốc độ cực đại của vật.
c) Tốc độ của vật ở thời điểm t = 1,5s
Ví dụ 2: Hình bên dưới là đồ thị vận tốc - thời gian của một vật dao động điều hòa.
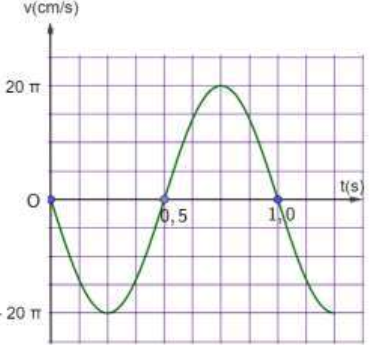
a) Xác định chu kì, tần số và tần số góc của vật
b) Tìm biên độ dao động của vật.
c) Xác định pha ban đầu của dao động.
d) Viết phương trình vận tốc của vật.
e) Kể từ lúc t = 0. Vật có tốc độ 10π cm/s lần đầu tiên ở thời điểm nào ?
Ví dụ 3: Một vật dao động điều hòa có đồ thị li độ - thời gian được cho ở hình bên.
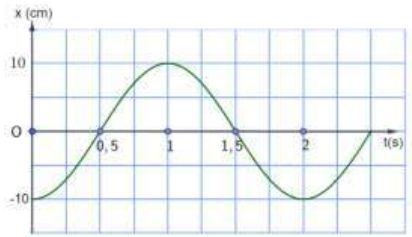
a) Viết phương trình vận tốc của vật.
b) Tính vận tốc của vật tại t = 1 (s)
Ví dụ 4: Một vật dao động điều hòa có phương trình li độ - thời gian được mô tả như hình bên. Biết rằng thời gian ngắn nhất giữa hai lần vật qua vị trí cân bằng (VTCB) là 0,5s
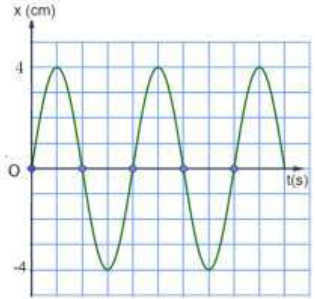
a) Viết phương trình dao động của vật. Từ đó suy ra phương trình vận tốc của vật.
b) Tính quãng đường vật đi được trong 1 chu kì dao động.
Ví dụ 5: Hình bên là đồ thị biểu diễn sự phụ thuộc của vận tốc v theo thời gian t của một vật dao động điều hòa.
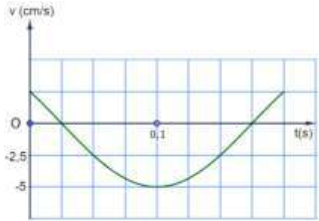
a) Xác định chu kì, tần số góc của dao động
b) Viết phương trình dao động của vật.
Ví dụ 6: Một vật dao động điều hòa có phương trình li độ \(x = 2\sqrt{2}\cos\left(10\pi t + \dfrac{3\pi}{4}\right)\), trong đó x tính bằng xentimét (cm) và t tính bằng giây (s). Tìm vị trí và hướng chuyển động của vật tại thời điểm t = 0
Ví dụ 7: Một vật dao động điều hòa có phương trình li độ \(x = 4\sin\left(2\pi t + \dfrac{\pi}{2}\right)\) (cm, s). Tìm vị trí và hướng chuyển động của vật tại thời điểm t = 0
Ví dụ 8: Một vật dao động điều hòa có phương trình vận tốc \(v = 20\pi \cos 5\pi t\) (cm/s).
a) Tìm biên độ dao động của vật
b) Viết phương trình dao động
c) Xác định vị trí và hướng chuyển động của vật tại thời điểm t = 0.
Ví dụ 9: Một vật dao động điều hòa có chu kì 2s, biên độ 10 cm.
a) Khi vật có li độ 5 cm thì tốc độ của vật bằng bao nhiều ?
b) Khi vật cách vị trí cân bằng \(5\sqrt{3}\) cm và đi theo chiều dương thì vận tốc của vật bằng ?
c) Khi vật có tốc độ \(5\pi\) cm/s thì vật cách vị trí cân bằng một đoạn bao nhiều ?
Ví dụ 10: Một vật dao động điều hòa trên trục Ox, quanh vị trí cân bằng O. Trong thời gian 31,4s chất điểm thực hiện được 100 dao động toàn phần. Biết lúc t = 0 vật qua vị trí có li độ \(2\sqrt{3}\) cm theo chiều dương với tốc độ là 40 cm/s. Lấy π = 3,14. Viết phương trình dao động của vật.
Ví dụ 11: Một vật dao động điều hòa với tần số 1 Hz. Tại thời điểm t = 0 vật qua vị trí có li độ 5 cm với vận tốc \(10\pi\) cm/s. Viết phương trình dao động của vật
III. GIA TỐC CỦA VẬT DAO ĐỘNG ĐIỀU HÒA
1. Phương trình gia tốc
\(a = v' = - {\omega ^2}A\cos \left( {\omega t + \varphi } \right)\) hoặc
\(a = {\omega ^2}A\cos \left( {\omega t + \varphi + \pi } \right)\)
\(a = -\omega^2 x\)
(Độ lớn gia tốc cực đại: \(a_{max} = \omega^2 A\))
2. Đặc điểm của gia tốc
Gia tốc của vật dao động cùng tần số góc, sớm pha π so với li độ (a và x ngược pha)
Gia tốc của vật dao động cùng tần số góc, sớm pha \(\dfrac{\pi}{2}\) so với vận tốc (a và v vuông pha)
Hệ thức quan hệ giữa gia tốc và vận tốc (Hệ thức vuông pha)
\(\dfrac{v^2}{v_{max}^2} + \dfrac{a^2}{a_{max}^2} = 1 \Rightarrow A^2 = \dfrac{v^2}{\omega^2} + \dfrac{a^2}{\omega^4}\)
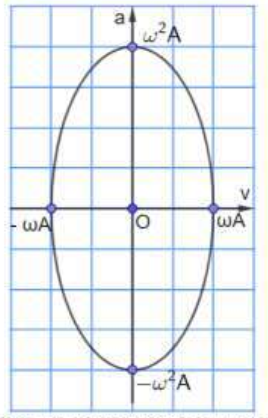
Đồ thị quan hệ giữa gia tốc a theo vận tốc v là 1 đường Elip
Các trường hợp đặc biệt
\(|v| = \dfrac{v_{max}}{2} \Leftrightarrow |a| = \dfrac{a_{max}\sqrt{3}}{2}\)
\(|v| = \dfrac{v_{max}\sqrt{3}}{2} \Leftrightarrow |a| = \dfrac{a_{max}}{2}\)
\(|v| = \dfrac{v_{max}\sqrt{2}}{2} \Leftrightarrow |a| = \dfrac{a_{max}\sqrt{2}}{2}\)
Vector gia tốc có chiều luôn hướng về VTCB
Gia tốc đổi chiều khi vật đi qua VTCB
Tại vị trí cân bằng a = 0
Khi vật đi qua biên dương thì gia tốc có giá trị nhỏ nhất \(a_{min} = -\omega^2 A\)
Khi vật đi qua biên âm thì gia tốc có giá trị cực đại \(a_{max} = \omega^2 A\)
Khi chất điểm chuyển động chậm dần thì a.v < 0 (a và v trái dấu hay ngược chiều)
Khi chất điểm chuyển động nhanh dần thì a.v > 0 (a và v cùng dấu hay cùng chiều)
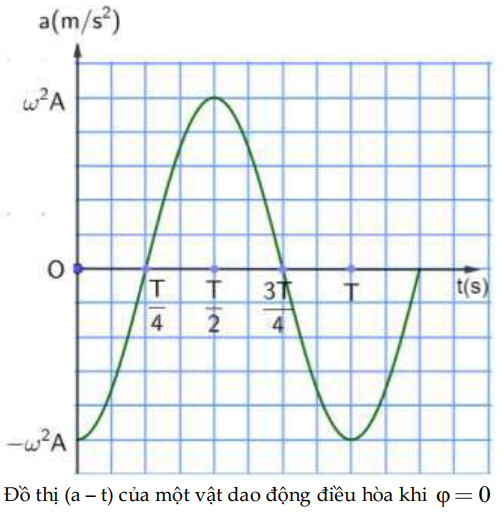
• Từ 0 → \(\dfrac{T}{4}\)
Vật chuyển động từ biên âm (\(a_{min} = -\omega^2 A\)) đến vị trí cân bằng (a = 0)
• Từ \(\dfrac{T}{4}\) → \(\dfrac{T}{2}\)
Vật chuyển động từ vị trí cân bằng (a = 0) đến vị trí biên dương (\(a_{max} = \omega^2 A\))
• Từ \(\dfrac{T}{2}\) → \(\dfrac{3T}{4}\)
Vật chuyển động từ vị trí biên dương \(a_{max} = \omega^2 A\) đến vị trí cân bằng a = 0
• Từ \(\dfrac{3T}{4}\) → T
Vật chuyển động từ vị trí cân bằng a = 0 đến vị trí biên âm \(a_{min} = -\omega^2 A\)
Ví dụ 1: Đồ thị li độ - thời gian của một vật dao động điều hòa được cho ở hình bên. Dựa vào đồ thị xác định:
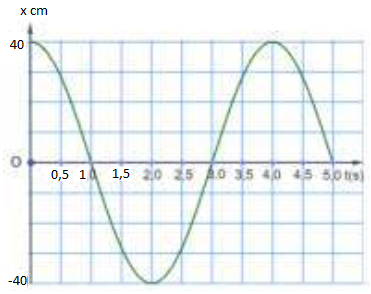
a) Gia tốc cực đại của vật
b) Viết phương trình gia tốc
c) Gia tốc của vật tại thời điểm t = 1,0 s
Ví dụ 2: Đồ thị vận tốc - thời gian của một vật dao động điều hòa được cho ở hình bên. Dựa vào đồ thị xác định:
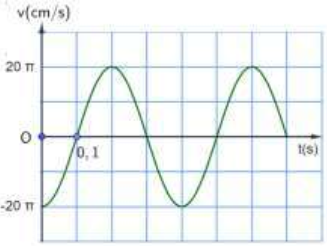
a) Chu kì, tần số và tần số góc của dao động.
b) Phương trình vận tốc của vật
c) Phương trình gia tốc của vật.
d) Li độ của vật tại t = 0
Ví dụ 3: Đồ thị gia tốc - thời gian của một vật dao động điều hòa được cho ở hình bên. Dựa vào đồ thị xác định:
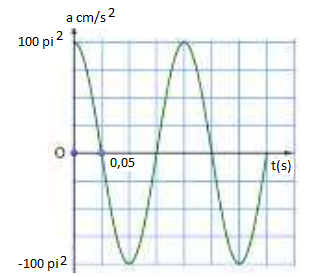
a) Chu kì, tần số và tần số góc của dao động.
b) Phương trình li độ của vật
c) Phương trình gia tốc của vật.
Ví dụ 4: Đồ thị hình bên mô tả liên hệ giữa gia tốc và li độ của một vật dao động điều hòa.
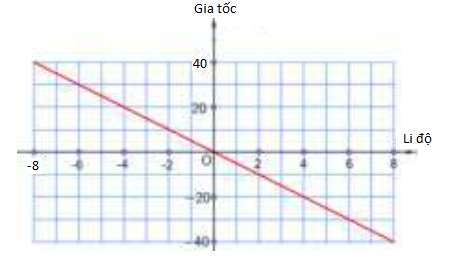
Sử dụng số liệu trong đồ thị hình bên để tính tần số của dao động
Ví dụ 5 (KNTT): Phương trình dao động của một vật là \(x = 5\cos 4t\) (cm). Hãy viết phương trình vận tốc và gia tốc của vật.
Ví dụ 6: Một chất điểm dao động điều hòa trên trục Ox. Khi chất điểm đi qua vị trí cân bằng thì có tốc độ là 20 cm/s. Khi chất điểm của nó có tốc độ là 10 cm/s thì gia tốc của nó có độ lớn là \(100\sqrt{3}\) cm/s². Tính biên độ dao động của vật ?
Ví dụ 7: Một chất điểm dao động điều hòa trên trục Ox. Khi chất điểm đi qua vị trí cân bằng thì tốc độ của nó là 20 cm/s. Khi chất điểm có tốc độ 10 cm/s thì gia tốc của nó có độ lớn là \(40\sqrt{3}\) cm/s². Biên độ dao động của chất điểm là ?
Ví dụ 8: Một chất điểm dao động điều hòa trên trục Ox. Khi chất điểm đi qua vị trí cân bằng thì tốc độ của nó là 30 cm/s. Khi chất điểm có tốc độ là 15 cm/s thì gia tốc của nó có độ lớn là \(90\sqrt{3}\) cm/s². Biên độ dao động của chất điểm là bao nhiều ?
Ví dụ 9: Một chất điểm dao động điều hòa có vận tốc cực đại 60 cm/s và gia tốc cực đại là \(2\pi\) (m/s²). Thời điểm ban đầu (t = 0) chất điểm có vận tốc 30 cm/s và đang chuyển động chậm dần. Chất điểm có gia tốc bằng π (m/s²) lần đầu tiên ở thời điểm nào ?
Ví dụ 10 (CTST): Một chất điểm dao động điều hòa với biên độ 4 cm, tần số 1 Hz. Tại thời điểm ban đầu, vật ở vị trí biên âm. Hãy xác định vận tốc và gia tốc của vật tại thời điểm t = 1 s, kể từ lúc bắt đầu chuyển động.
Ví dụ 11 (CTST): Một vật dao động điều hòa có đồ thị gia tốc theo thời gian a(t), được cho bởi đồ thị như hình
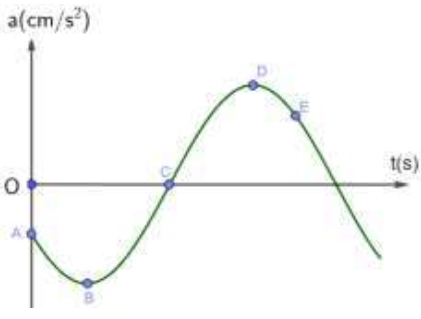
a) Điểm nào trên đồ thị thể hiện vật đang ở vị trí biên dương +A
b) Tại điểm C, vật đang có vận tốc dương, âm hay bằng không ?
c) Tại điểm E, vị trí vật đang ở biên dương +A, biên âm -A, vị trí cân bằng, trong khoảng -A;0 hay trong khoảng 0;+A ?