Tính đơn điệu và cực trị của hàm số - phần 1
**Chương 01 - Bài 1: TÍNH ĐƠN ĐIỆU & CỰC TRỊ CỦA HÀM SỐ**
**A. Lý thuyết**
**1. Tính đơn điệu, nghịch biến của hàm số**
**Định nghĩa:**
Kí hiệu K là khoảng; đoạn; nửa khoảng. Giả sử hàm số \(y = f(x)\) xác định trên K.
Hàm số \(y = f(x)\)
• Gọi là đồng biến trên K nếu \(\forall x_1, x_2 \in K\) mà \(x_1 < x_2\) thì \(f(x_1) < f(x_2)\).
• Gọi là nghịch biến trên K nếu \(\forall x_1, x_2 \in K\) mà \(x_1 < x_2\) thì \(f(x_1) > f(x_2)\).
**Chú ý:**
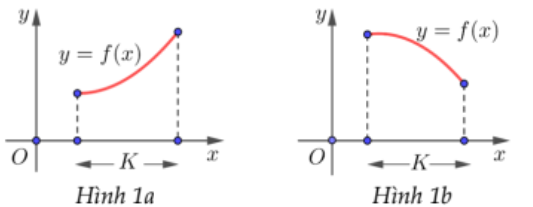
» Hàm số \(y = f(x)\) đồng biến trên K thì đồ thị đi lên từ trái sang phải (Hình 1a).
» Hàm số \(y = f(x)\) nghịch biến trên K thì đồ thị đi xuống từ trái sang phải (Hình 1b).
**2. Tính đơn điệu của hàm số**
**Định lý:**
Cho hàm số \(y = f(x)\) có đạo hàm trên K.
• Nếu \(f'(x) > 0\) với mọi x thuộc K thì hàm số \(y = f(x)\) đồng biến trên K.
• Nếu \(f'(x) < 0\) với mọi x thuộc K thì hàm số \(y = f(x)\) nghịch biến trên K.
**Chú ý:**
» Định lí vẫn đúng trong trường hợp \(f'(x) = 0\) tại một số hữu hạn điểm trong K.
» Nếu \(f'(x) = 0\) với mọi \(x \in K\) thì hàm số \(f(x)\) không đổi trên khoảng K.
**3. Khái niệm cực trị của hàm số**
**Định nghĩa:**
Cho hàm số \(y = f(x)\) xác định và liên tục trên khoảng \((a;b)\) (a có thể là \(-\infty\), b có thể là \(+\infty\)) và điểm \(x_0 \in (a;b)\).
• \(\exists h > 0\) sao cho \(f(x) < f(x_0)\) với mọi \(x \in (x_0 - h; x_0 + h) \subset (a;b)\) và \(x \neq x_0\) thì ta nói hàm số \(f(x)\) đạt **cực đại** tại \(x_0\).
• \(\exists h > 0\) sao cho \(f(x) > f(x_0)\) với mọi \(x \in (x_0 - h; x_0 + h) \subset (a;b)\) và \(x \neq x_0\) thì ta nói hàm số \(f(x)\) đạt **cực tiểu** tại \(x_0\).
**Chú ý:**
» Hàm số \(y = f(x)\) đạt cực đại tại \(x_0\) thì \(x_0\) được gọi là **điểm cực đại** của hàm số \(f(x)\).
Khi đó, \(f(x_0)\) được gọi là **giá trị cực đại** của hàm số \(f(x)\) và kí hiệu là \(f_{CĐ}\) hay \(y_{CĐ}\).
Điểm \(M_0(x_0; f(x_0))\) được gọi là **điểm cực đại** của đồ thị hàm số.
» Hàm số \(y = f(x)\) đạt cực tiểu tại \(x_0\) thì \(x_0\) được gọi là **điểm cực tiểu** của hàm số \(f(x)\).
Khi đó, \(f(x_0)\) được gọi là **giá trị cực tiểu** của hàm số \(f(x)\) và kí hiệu là \(f_{CT}\) hay \(y_{CT}\).
Điểm \(M_0(x_0; f(x_0))\) được gọi là **điểm cực tiểu** của đồ thị hàm số.
» Các điểm cực đại và điểm cực tiểu được gọi chung là điểm cực trị.
Giá trị cực đại và giá trị cực tiểu được gọi chung là **giá trị cực trị** (cực trị) của hàm số.
**4. Cách tìm cực trị của hàm số**
**Định lý:**
Giả sử hàm số \(y = f(x)\) liên tục trên khoảng \((a;b)\) chứa điểm \(x_0\) và có đạo hàm trên các khoảng \((a;x_0)\) và \((x_0;b)\). Khi đó:
• Nếu \(f'(x) < 0\) với mọi \(x \in (a;x_0)\) và \(f'(x) > 0\) với mọi \(x \in (x_0;b)\) thì \(x_0\) là một điểm cực tiểu của hàm số \(f(x)\)
• Nếu \(f'(x) > 0\) với mọi \(x \in (a;x_0)\) và \(f'(x) < 0\) với mọi \(x \in (x_0;b)\) thì \(x_0\) là một điểm cực đại của hàm số \(f(x)\).
» Định lí trên được viết gọn lại trong hai bảng biến thiên sau:
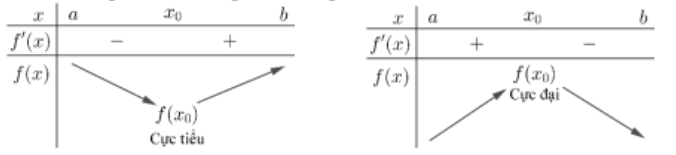
**Chú ý:**
» Từ định lí trên ta có các bước tìm cực trị của hàm số \(y = f(x)\) như sau:
**(1)** Tìm tập xác định của hàm số.
**(2)** Tính \(f'(x)\). Tìm các điểm mà tại đó \(f'(x)\) bằng 0 hoặc \(f'(x)\) không tồn tại.
**(3)** Lập bảng biến thiên suy ra các cực trị của hàm số.
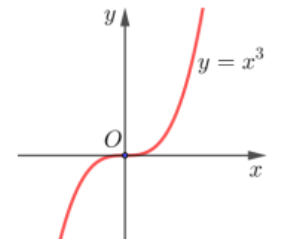
» Nếu \(f'(x_0) = 0\) nhưng \(f'(x)\) không đổi dấu khi x qua \(x_0\) thì \(x_0\) không phải là điểm cực trị của hàm số.
Chẳng hạn, hàm số \(f(x) = x^3\) có \(\begin{cases} f'(x) = 3x^2 \\ f'(0) = 0 \end{cases}\), nhưng \(x = 0\) không phải là điểm cực trị của hàm số.
**B. Các dạng bài tập**
**Dạng 1. Xét tính đơn điệu của hàm số cho bởi một công thức****Phương pháp:**
» **Bước 1:** Tìm tập xác định D của hàm số.
» **Bước 2:** Tính đạo hàm \(f'(x)\) của các hàm số. Tìm các điểm \(\{x_1; x_2; ...; x_n\} \in D\) mà tại đó đạo hàm \(f'(x)\) bằng 0 hoặc không tồn tại.
» **Bước 3:** Sắp xếp các điểm \(x_1; x_2; ...; x_n\) theo thứ tự tăng dần. Xét dấu \(f'(x)\) và lập bảng biến thiên.
» **Bước 4:** Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.
**Ví dụ 1.1.**
Xét tính đơn điệu của hàm số \(y = 4x^3 + 3x^2 - 36x + 6\).
**Ví dụ 1.2.**
Xét tính đơn điệu của hàm số \(f(x) = \dfrac{x-1}{x+1}\).
**Ví dụ 1.3.**
Xét tính đơn điệu của hàm số \(y = \sqrt{-x^2 + 4}\).
**Ví dụ 1.4.**
Xét tính đơn điệu của hàm số \(y = \log_3(x^2 - 2x)\).
**Dạng 2. Xét tính đơn điệu của hàm số cho bởi đồ thị - bảng biến thiên**
**Phương pháp:**
» Với đồ thị hàm số, quan sát: hướng lên – xuống của **đường cong** (chiều từ trái sang phải).
» Với bảng biến thiên, quan sát: hướng lên – xuống của **mũi tên** (chiều từ trái sang phải).
» Với bảng xét dấu, quan sát: dấu âm - dương của \(f'(x)\).
**Ví dụ 2.1.**
Cho hàm số \(y = f(x)\) xác định trên \(\mathbb{R}\) và có bảng biến thiên như sau:
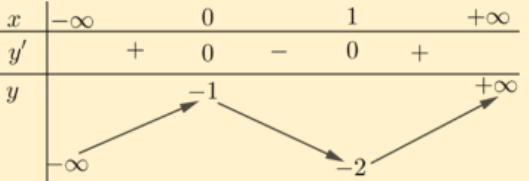
Xét tính đơn điệu của hàm số \(y = f(x)\).
**Ví dụ 2.2.**
Cho hàm số \(y = f(x)\) liên tục trên đoạn \([-3;3]\) và có đồ thị như hình bên.
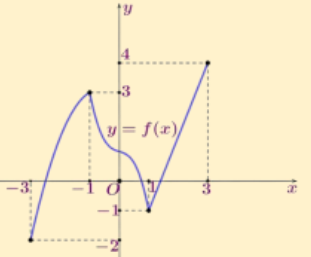
Xét tính đơn điệu của hàm số \(y = f(x)\).
**Dạng 3. Xác định cực trị của hàm số cho bởi công thức****Phương pháp:**
» **Bước 1:** Tìm tập xác định D của hàm số.
» **Bước 2:** Tính đạo hàm \(f'(x)\) của các hàm số. Tìm các điểm \(\{x_1; x_2; ...; x_n\} \in D\) mà tại đó đạo hàm \(f'(x) = 0\) hoặc \(f'(x)\) không tồn tại.
» **Bước 3:** Sắp xếp các điểm \(x_1; x_2; ...; x_n\) theo thứ tự tăng dần. Xét dấu \(f'(x)\) và lập bảng biến thiên.
» **Bước 4:** Kết luận hàm số đạt cực trị tại \(x = ?\), \(y = ?\) (nếu có).
Tìm cực trị của hàm số \(y = 2x^3 - 3x^2 + 1\)
**Ví dụ 3.2.**
Tìm cực trị của hàm số \(y = -x^4 + 2x^2 - 2x - 1\)
**Ví dụ 3.3.**
Tìm cực trị của hàm số \(y = \dfrac{x + 2}{3x - 1}\)
**Ví dụ 3.4.**
Tìm cực trị của hàm số \(y = \dfrac{x^2 - 4x + 4}{1 - x}\)
**Ví dụ 3.5.**
Tìm cực trị của hàm số \(f(x) = 2^{x^2-5x}\)
**Dạng 4. Xác định cực trị của hàm số cho bởi bảng biến thiên – đồ thị**
**Phương pháp:**
**Nhận xét:**

Hình minh họa:
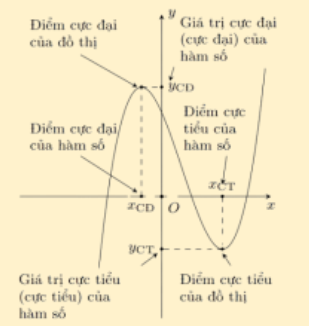
» Đối với một hàm số bất kì, hàm số chỉ có thể đạt cực trị tại những điểm \(x_0\) mà tại đó đạo hàm triệt tiêu \(f'(x_0) = 0\) hoặc đạo hàm không xác định tại đó.
**Ví dụ 4.1.**
Cho hàm số \(y = f(x)\) có đạo hàm trên \(\mathbb{R}\) và đồ thị hàm số \(y = f'(x)\) như hình bên. Đồ thị hàm số \(y = f(x)\) bao nhiêu có điểm cực tiểu và điểm cực đại?
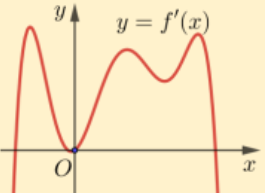
**Ví dụ 4.2.**
Cho hàm số \(y = f(x)\) có bảng biến thiên như sau:
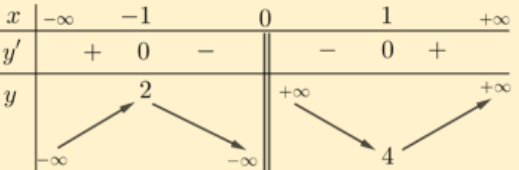
Hàm số \(y = f(x)\) bao nhiêu có điểm cực tiểu và điểm cực đại?
**Ví dụ 4.3.**
Cho hàm số \(y = f(x) = ax^3 + bx^2 + cx + d\) có bảng biến thiên như sau:
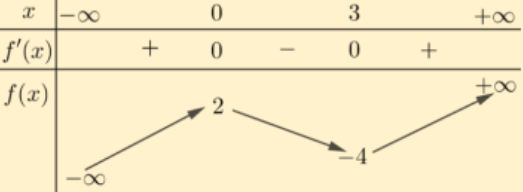
Dựa vào bảng biến thiên, hãy thiết lập công thức hàm số \(y = f(x)\) đã cho?