CD-Bài 1-Góc lượng giác, giá trị lượng giác của góc LG
§1 GÓC LƯỢNG GIÁC. GIÁ TRỊ LƯỢNG GIÁC CỦA GÓC LƯỢNG GIÁC
Trên mặt chiếc đồng hồ, kim giây đang ở vị trí ban đầu chỉ vào số 3 (Hình 1).

Kim giây quay ba vòng và một phần tư vòng (tức là 3\(\dfrac{1}{4}\) vòng) đến vị trí cuối chỉ vào số 6.
Khi quay như thế, kim giây đã quét một góc với tia đầu chỉ vào số 3, tia cuối chỉ vào số 6.
Góc đó gọi nên khái niệm gì trong toán học? Những góc như thế có tính chất gì?
I. GÓC LƯỢNG GIÁC
1. Góc hình học và số đo của chúng
- Góc (còn được gọi là góc hình học) là hình gồm hai tia chung gốc. Mỗi góc có một số đo, đơn vị đo góc là độ.
- Nếu ta chia đường tròn thành 360 cung tròn bằng nhau thì góc ở tâm chắn mỗi cung đó là 1°.
- Số đo của một góc (hình học) không vượt quá 180°.
- Một đơn vị khác được sử dụng nhiều khi đo góc là radian (đọc là ra-đi-an).
- Nếu trên đường tròn, ta lấy một cung tròn có độ dài bằng bán kính thì góc ở tâm chắn cung đó gọi là góc có số đo 1 radian, gọi tắt là góc 1 radian (Hình vẽ).
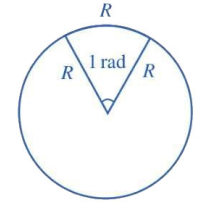
- 1 radian còn viết tắt là 1 rad.
Chú ý: \(\boxed{\pi \,\,\left( {rad} \right) = {{180}^o}}\)
- Để đổi từ rad sang độ hoặc từ độ sang rad ta dùng quy tắc tam suất
Ví dụ: từ \({18^o}\) đổi sang \(rad\):
\({180^o} = \pi \,\,rad\)
\({18^o} = ?\,\,\,rad\)
\(? = \dfrac{{{{18}^o}.\pi }}{{{{180}^o}}}\,\,rad = \dfrac{\pi }{{10}}rad\)
Ví dụ: từ \(\dfrac{{2\pi }}{9}\) đổi sang độ
\(\pi \,\,rad = {180^o}\)
\(\dfrac{{2\pi }}{9} = ?\,\,độ\)
\(? = \dfrac{{2\pi }}{9}.\dfrac{{{{180}^o}}}{\pi } = {40^o}\)
2. Góc lượng giác và số đo của chúng
a) Khái niệm
- Trong góc lượng giác, chiều dương là chiều ngược chiều quay của kim đồng hồ, chiều âm là chiều cùng chiều quay của kim đồng hồ.
|
|---|
Ví dụ. Đọc tên góc lượng giác, tia đầu và tia cuối của góc lượng giác đó trong hình sau:
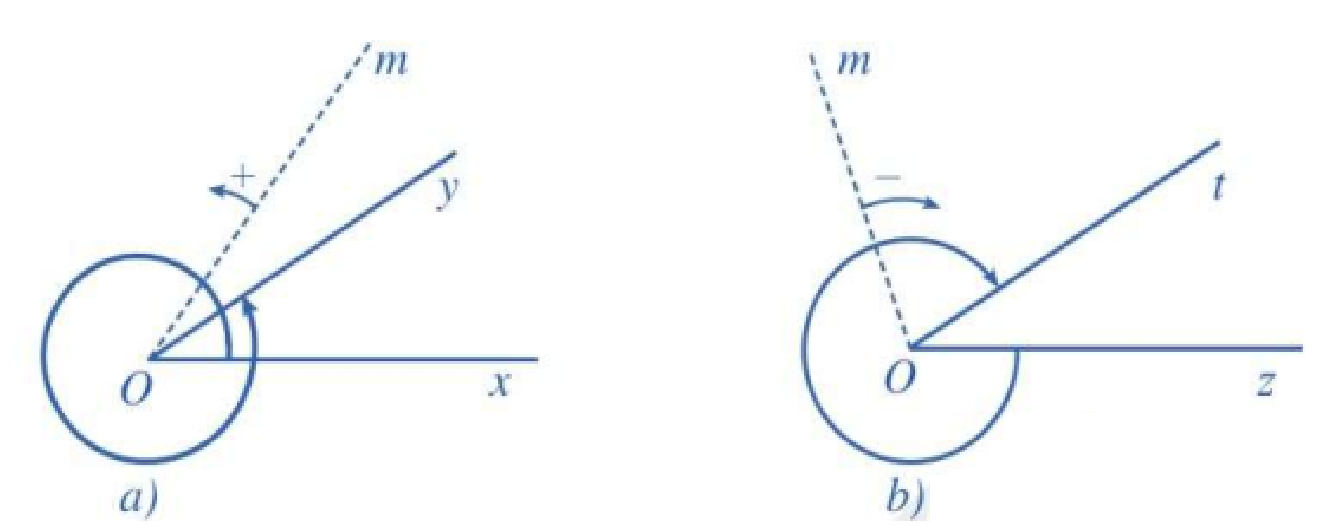
Hình a) góc LG là \(\left( {Ox,Oy} \right)\). Tia đầu là \(Ox\), tia cuối là \(Oy\)
Hình b) góc LG là \(\left( {Oz,Ot} \right)\). Tia đầu là \(Oz\), tia cuối là \(Ot\)
Ví dụ:
a) Trong Hình a, tia Om quay theo chiều dương đúng một vòng. Hỏi tia đó quét nên một góc bao nhiều độ?
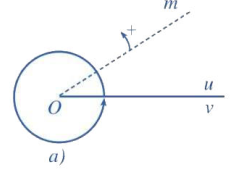
Quét một góc \({360^o}\)
b) Trong Hình b, tia Om quay theo chiều dương ba vòng và một phần tư vòng (tức là 3\(\dfrac{1}{4}\) vòng). Hỏi tia đó quét nên một góc bao nhiều độ?
Quét một góc \({1170^o}\)
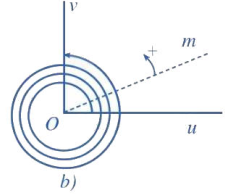
c) Trong Hình c, tia Om quay theo chiều âm đúng một vòng. Hỏi tia đó quét nên một góc bao nhiều độ?
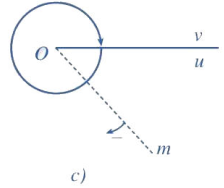
Quét một góc \( - {360^o}\)
- Nhận xét: Khi tia Om quay góc α⁰ thì góc lượng giác mà tia đó quét nên có số đo α⁰ (hay \(\dfrac{πα}{180}\) rad). Vì thế, mỗi một góc lượng giác đều có một số đo, đơn vị đo góc lượng giác là độ hoặc radian.
- Nếu góc lượng giác \((Ou, Ov)\) có số đo bằng α thì ta kí hiệu là \(sđ(Ou, Ov) = α\) hoặc \((Ou, Ov) = α\).
|
|---|
Ví dụ. Hãy biểu diễn trên mặt phẳng góc lượng giác trong mỗi trường hợp sau:
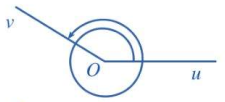
a) Góc lượng giác gốc O có tia đầu Ou, tia cuối Ov và có số đo 510°;
\(510° = 360° + 150°\)
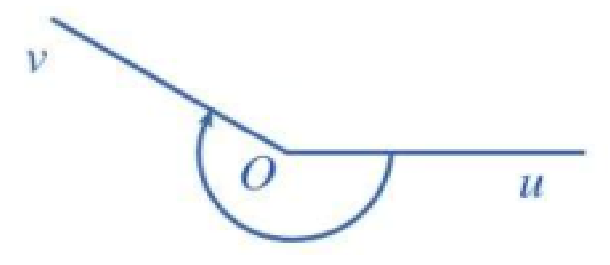
b) Góc lượng giác gốc O có tia đầu Ou, tia cuối Ov và có số đo \(-\dfrac{7π}{6}\).
\(-\dfrac{7π}{6} = -π + (-\dfrac{π}{6})\)
b) Tính chất
Với hai tia \(Oa\) và \(Ob\) cho trước, có vô số góc lượng giác tia đầu \(Oa\) và tia cuối \(Ob\). Ta dùng chung kí hiệu \((Oa, Ob)\) cho tất cả các góc lượng giác này.
Số đo của các góc lượng giác có cùng tia đầu \(Oa\) và tia cuối \(Ob\) sai khác nhau một bội nguyên của 360° nên có công thức tổng quát là:
\(sđ(Oa, Ob) = α° + k 360° (k ∈ ℤ)\), thường viết là \((Oa, Ob) = α° + k 360°\)
với \(α°\) là số đo của một góc lượng giác bất kì có tia đầu \(Oa\) và tia cuối \(Ob\).
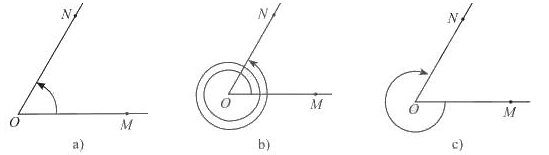
Ví dụ: Cho \(\widehat{MON}\) = 60°. Xác định số đo của các góc lượng giác được biểu diễn trong hình và viết công thức tổng quát của số đo góc lượng giác (OM, ON).
Ví dụ: Trong các khoảng thời gian từ 0 giờ đến 2 giờ 15 phút, kim phút quét một góc lượng giác là bao nhiều độ?
Hệ thức Chasles (Sa-lơ)
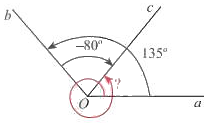
a) Xác định số đo các góc lượng giác (Oa, Ob), (Ob, Oc) và (Oa, Oc)
b) Nhận xét về mối liên hệ giữa ba số đo góc này.
Ta thừa nhận hệ thức sau về số đo của góc lượng giác, gọi là hệ thức Chasles:
Với ba tia Oa, Ob và Oc bất kì, ta có
\((Oa, Ob) + (Ob, Oc) = (Oa, Oc) + k 360° (k ∈ ℤ)\).
